A Deep Dive Into the Criss-Cross Multiplication Algorithm
A concise explanation of the criss-cross multiplication algorithm and its implementation in C++.
Back in 2019, I stumbled upon the criss-cross multiplication algorithm on Youtube. It comes from Vedic mathematics, a compendium of tricks for increasing the speed of mathematical calculations. The distinguishing feature of this algorithm is the fact that it can be used for mental calculations and it is much faster than the grade-school multiplication algorithm.
The implementation of the criss-cross multiplication algorithm in C++ can be done in about 50 lines of code and it manages to multiply 1000-digit numbers in string format almost instantly. Moreover, when multiplying numbers having less than 1000 digits, it is nearly twice as fast as the Karatsuba algorithm, one of the most popular fast multiplication algorithms in computer science.
Algorithm
Depending on the number of digits to be multiplied, there is a specific sequence of patterns to follow when carrying out the single digit products.
For each pattern:
- Compute the sum of all the required single digit products as indicated by the pattern.
- Add the carry from the previous step, if any, to this sum.
- Prepend the unit’s digit (last digit) of the sum to the answer.
- Update carry to the remaining digits in the sum.
- Move to the next pattern.
Pattern for 2-digit multiplication
In the following GIFs, the dots represent the digits and each line represent the product of 2 digits.
Detailed explanation for $29 \times 12$
Pattern for 3-digit multiplication
Pattern for 4-digit multiplication
Pattern for 5-digit multiplication
Things to note
Make use of symmetry to remember the sequence of patterns. For example, notice that the last $n/2$ patterns are simply a reflection in the vertical axis of the first $n/2$ patterns.
When the 2 numbers being multiplied have different lengths, simply prepend zeros to the smaller number to make it the same length as the larger number. For example, the criss-cross multiplication of $512323$ and $32$ is the same as the criss-cross multiplication of $512323$ and $000032$. In such a case, you will notice that there will be fewer single-digit products to carry out.
Proof
Even though I have not found a formal proof for the correctness of the criss-cross algorithm, we can get some insights into why it works by comparing it side-by-side with the grade-school algorithm :
We are doing the exact calculations as the grade-school multiplication algorithm. The difference lies in the order in which these calculations are carried out : the criss-cross algorithm uses a more efficient order which allows us to work with smaller numbers and gradually build the answer at each step.
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
std::string vedic(std::string a, std::string b) {
if (a == "0" || b == "0") return "0";
if (b.length() > a.length()) {
std::string t = b;
b = a;
a = t;
}
const long long asize = static_cast<long long>(a.size());
const long long bsize = static_cast<long long>(b.size());
long long totalsteps = asize + bsize - 1;
std::string ans = "";
long long max = asize - 1, min = bsize - 1;
long long sum = 0, carry = 0;
long long lines = 0; // number of multiplications at each step
// Each step finds 1 digit of the answer
for (long long step = 1; step <= totalsteps; step++) {
sum = 0; // reset sum
if (step <= asize) {
lines = step;
} else {
lines = asize - (step - asize);
}
if (min < 0) {
min = 0;
max--;
if (step < asize) {
lines -= step - bsize;
} else {
lines -= asize - bsize;
}
}
long long i = max, j = min;
for (long long k = 0; k < lines; k++) {
sum += (a[i] - '0') * (b[j] - '0');
i--;
j++;
}
sum += carry;
carry = sum / 10;
ans = std::to_string(sum % 10) + ans;
min--;
}
if (carry != 0) ans = std::to_string(carry) + ans;
return ans;
}
Time complexity : $\mathbb O (n^2)$.
Space complexity : $\mathbb O (m + n) $ where $m$ and $n$ are the number of digits in the multiplier and multiplicand respectively.
Explanation
1
2
3
4
5
6
ll i = max, j = min;
for (ll k = 0; k < lines; k++) {
sum += (a[i] - '0') * (b[j] - '0');
i--; j++;
}
$min$ and $max$ keep track of the region within which the cross-multiplication will take place.
$i$ : pointer used to iterate over $a$ within the range $[min, max]$.
$j$ : pointer used to iterate over $b$ within the range $[min, max]$.
Case 1 : Both $a$ and $b$ have $n$ digits
This is the simplest case. The total number of steps required is $2n-1$. (There are $n$ patterns + $n$ reflected patterns. However, the $n$-th pattern is counted twice so we minus $1$.)
The number of single digit product (or the number of lines drawn) at each step can be found as follows :
1
2
if (currentstep <= n) {lines = currentstep;}
else {lines = n - (currentstep - n);} // or 2*n - currentstep
| Step number | Number of single digit product required |
|---|---|
| $ 1 $ | $1 $ |
| $ 2 $ | $ 2 $ |
| $ 3 $ | $3 $ |
| $ 4 $ | $4 $ |
| $ … $ | $ … $ |
| $ n $ | $n $ |
| $n+1$ | $n-1$ |
| $n+2 $ | $n-2 $ |
| $n+3$ | $n-3 $ |
| $… $ | $…$ |
| $ 2n-1 $ | $ 1 $ |
At each step, we will compute the sum of all the 1-digit multiplications required. From this sum we will obtain the carry for the next step and a digit of our answer.
Pseudocode for Case 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Initialise the total number of steps
Initialise min and max to n-1
For each step
Determine the number of 1-digit multiplication to be carried out
Initialise sum to 0
When the step number becomes > n (or when min becomes negative), set min to 0 and decrement max.
For each 1-digit multiplication
Increment sum
Modify counters to move to next 1-digit multiplication
Add previous carry to sum
Update carry and answer
Decrement min
If carry is non-zero, concatenate it to the left of the answer.
Return answer
Case 2 : $b$ has fewer digits than $a$
This case could be eliminated if we simply make both $a$ and $b$ the same length initially by adding leading zeros to $b$. However, this approach is time-consuming because there will be unnecessary and will introduce leading zeros in our final answer which must be removed.
To bypass this problem, we simply reduce the total number of steps and the number of single digit products at each step to eliminate cases where the 1-digit multiplication involves a leading zero.
The total number of steps is now found using :
\[\boxed{\text{totalsteps = length(a) + length(b) - 1}}\]For each step, we first find the expected number of 1-digit multiplication if $a$ and $b$ were the same length :
1
2
3
4
5
6
if (step <= asize) {
lines = step;
}
else {
lines= asize - (step- asize); // do not simplify as 2*asize might overflow
}
When all the digits of $b$ have been traversed, $min$ becomes negative. Previously when $a$ and $b$ were the same length, we exited when $min$ was negative. However, when they differ in length, we cannot exit. Now, each time $min$ reaches the start of $b$, we decrement $max$ and keep $min$ at index 0 of $b$.
1
2
3
4
if (min < 0) {
min = 0;
max--;
}
Then we reduce the number of 1-digit multiplication as follows :
1
2
3
4
5
6
7
8
9
10
if (min < 0) {
min = 0;
max--;
if (step < asize) {
lines -= step - bsize;
}
else {
lines -= asize - bsize;
}
}
The rest of the code for Case 2 is the same as that in Case 1.
Comparison with Karatsuba
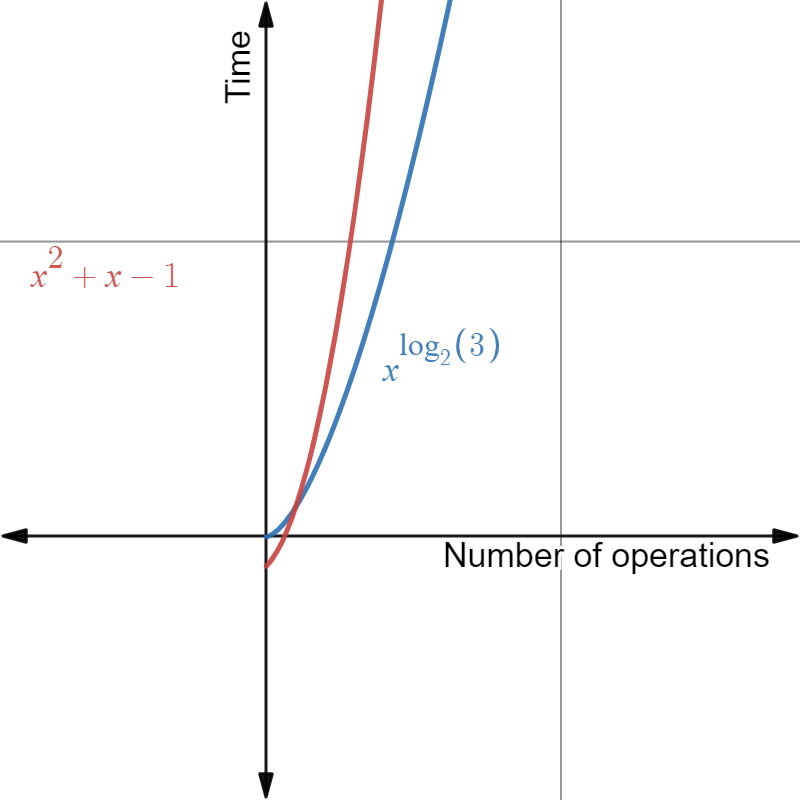
From the table in Case 1, we can deduce that the total number of single digit products carried out by the criss-cross algorithm is \(n^2 + n - 1\). In comparison, the total number of single digit products for the Karatsuba algorithm is \(n^{\log_2 3}\).
In theory, as the numbers being multiplied tend to infinity, the Karatsuba algorithm will perform better. But for relatively small numbers, the Karatsuba algorithm actually performs worse.
Based on my own benchmarks which should be taken with a grain of salt, the criss-cross algorithm performs better when the multiplicand and multiplier have less than 100 digits. For example, for 10-digit multiplication, the criss-cross algorithm seems to take 50% less time than the Karatsuba algorithm.
Final thoughts
The criss-cross algorithm is much simpler to understand than the Karatsuba algorithm. It is also more suitable for mental calculations. However, it is not suitable for multiplying numbers tending to infinity.
All code used in this post can be found on Github.